Wirtschafts- und Finanzpolitik
wo jeder alles besser weiß.
Hanns Dieter Hüsch
Freie Meinungen, freizügige Interpretation von Nachrichten und erfundene Behauptungen haben in den sogenannten sozialen Medien zu Verwirrung und Desinformation geführt. Dabei geraten wissenschaftlich gesicherte Erkenntnisse in den Hintergrund. Dass zum Beispiel prozentuales Wirtschaftswachstum, wie es permanent gefordert wird, in eine umfassende Katastrophe führt, ist eine mathematisch gesicherte Erkenntnis, von der wir aber nur Einzelaspekte wahrnehmen:
Plastikmüll im Meer, Insektensterben oder Gletscherschmelze.
Was machen Physiker und Naturwissenschaftler seit den Zeiten von Galilei, wenn sie ein Phänomen in der Natur erkannt haben?
Sie wenden Mathematik an und versuchen, die Fakten in einen funktionalen Zusammenhang zu stellen und dann mathematisch zu bearbeiten. Mit den mathematisch erzielten Ergebnissen, den Formeln und Funktionen, versuchen sie dann, auch weitere Probleme zu lösen. Die Mathematik, die dabei zur Anwendung kommt, ist wenigstens zweihundert Jahre alt und gilt als Basiswissen, welches Studierenden der Mathematik, Informatik, Physik und der meisten Ingenieurwissenschaften in den ersten vier Semestern vermittelt wird.
Ein Beispiel ist der Begriff Erneuerbare Energien, der physikalisch gesehen, ziemlicher Unsinn ist. Jede Energie ist in alles Mögliche umwandelbar, also man könnte auch sagen, Energie ist fast immer erneuerbar. Gemeint ist aber etwas anderes: Energie, die nicht aus Bodenschätzen gewonnen wird.
Das Erneuerbare ist kein Kriterium für Energie. Und viele denken dann, erneuerbare Energie kommt aus der Steckdose. Es wird auch vorgetäuscht, dass aus der gleichen Stromleitung erneuerbare oder nicht erneuerbare Energie fließen könnte, und das wäre dann nur eine Frage des Anbieters, der Wahl des Konsumenten und des Preises pro Kilowattstunde.
Mit anderen Worten, das Problem mit der Energie wäre nur eine Frage des Geldes. Das bedeutet, Geld hätte eine alles entscheidende Funktion in der Energiewirtschaft, mit viel Geld könnte man alle Probleme lösen. Dabei ist es genau umgekehrt: Energie hat eine entscheidende Funktion in der Geldwirtschaft, es wird da investiert, wo Energie herkommt. Wenn wir uns entscheiden, Solarenergie zu verwenden, wird die Geldwirtschaft in Solarenergie investieren.
ist eine Form von Denkfaulheit
oder Dummheit.
Was ist eine Funktion?
Mathematik für alle
Ein funktionaler Zusammenhang besteht zwischen der Zeugung eines Kindes und der Geburt. Zwischen der Urnen-Wahl und der Zusammensetzung eines Parlamentes. Zwischen einem Bombenabwurf und den zivilen Kriegstoten.
Ein funktionaler Zusammenhang bedeutet: Der Zusammenhang zwischen einer bekannten Ausgangslage und einem unbekannten (oder auch schon bekannten) Ergebnis kann durch mathematische Funktionen beschrieben werden.
Der funktionale Zusammenhang ist in der Regel eindeutig, jedem Wert auf der einen Seite wird ein Wert auf der anderen Seite zugeordnet. Dabei kann es vorkommen, dass die Berechnung der betreffenden Funktion sehr aufwändig und vielen Außenstehenden unzugänglich ist. Das ändert aber nichts an der Zuverlässigkeit der Aussage, auch, wenn sie schwer zu vermitteln oder gewöhnungsbedüftig ist.
Aber, wer sich nicht damit beschäftigt hat und auch jetzt nicht beschäftigen will, hat nicht die Kompetenz und das Recht, die vorhandenen Zusammenhänge zu leugnen.
Die unerbittliche Wachstumsfunktion
Mathematik für alle
Zu den Funktionen, die man - wenigstens grob - kennen sollte, gehören die Exponentialfunktionen. Deren Wesen und Struktur ist selbst vielen Akademikern unbekannt. (Ein Beispiel für eine Akademikerin in höchster Position, welche Exponentialfunktionen offenbar nicht zur Kenntnis nimmt, wird weiter unten gegeben.)
Das Wesen einer Wachstumsfunktion ist nicht schwer zu verstehen: Der Zuwachs der Menge (Algen, Insekten-Population bei genügender Nahrung, Krebszellen im Körper) ist der vorhandenen Menge proportional. Proportional bedeutet, die Menge wird mit einem konstanten Faktor multipliziert, sie wächst zum Beispiel in einem Jahr um soundsoviel Prozent.
f ' (x) = a f(x)
f ' (x) = 2% f(x)
Und jetzt gehen wir direkt in die Ökonomie und in die Politik. Sagen wir, f(x) sei das Bruttosozialprodukt oder irgendeine Größe, die das Volumen unserer Wirtschaft beschreibt, in Euro gemessen. Es wird gefordert, dass das jährliche Wirtschaftswachstum zwei Prozent der vorhandenen Wirtschaftsleistung sein soll.
Was bedeutet das?
f ' (x) = a f(x)
Dabei ist a = 2 Prozent.
Die muss nicht jeder lösen können. Doch Mathematiker können das seit 200 Jahren. Das Ergebnis ist eine Exponentialfunktion.
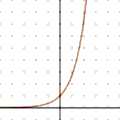
Jede Exponentialfunktion hat folgende Eigenschaften: Sie steigt, erst langsam, dann immer schneller, weil der Anstieg (dem vorhandenen Wert proportional) immer größer wird. Die Funktion hat kein Maximum, sie wächst immer weiter, ändert nie ihre Richtung, wird immer steiler und steiler und geht schnell gegen unendlich. Das Bild so einer Exponentialfunktion hat wohl jeder schon gesehen.
Nicht so die Akteure im Finanzsektor. Das Postulat vom prozentualen Wachstum geht nämlich von der Finanzwirtschaft aus. Seit Jahrhunderten denkt man in dieser Branche prozentual. Es beginnt damit, dass Zinsen immer in Prozenten pro Jahr gefordert werden und es scheint, dass den Bankern und Finanzakteuren die Mathematik jenseits der Prozentrechnung unbekannt ist.
Was lernen wir daraus? Die Forderung nach Wirtschaftswachstum von ein, zwei oder drei Prozent (oder jedem anderen positiven Wert) führt automatisch zu einem exponentiellen Wachstum der Wirtschaft ins Unendliche. Wie ein Krebsgeschwür.
- Das fällt erst dann auf, wenn uns in Einzelbereichen das Ergebnis nicht gefällt:
- zu viel Kohlendioxid in der Atmosphäre,
- zu viel Plastik im Ozean,
- zu viele Autos auf den Straßen,
- zu viel Gift auf den Feldern,
- zu viele Kilos auf den Beinen,
- zu viele Waffen in der Hand von Fanatikern
- zu viel militärische Rüstung in den USA, die bekanntlich in allen Bereichen des Wachstums das Maximum für sich einfordern. Das ist der sogenannte Exzeptionalismus der USA.
Dass auch unser bescheideneres Wirtschaftswachstum von zwei Prozent nicht nur in den genannten Beispielen, sondern in jedem Fall in einem funktionalen Zusammenhang mit dem Ausarten ins Übermaß steht, das wird systematisch ignoriert.
Exponentielles Wirtschaftswachstum führt zur Ausbeutung aller Ressourcen an Material und Energie auf diesem Planeten und zur Ausbeutung aller menschlichen Kräfte.
Die Menge des vorhandenen Geldes wird ständig, global, Tag und Nacht vergrößert. Die Lage ist unübersichtlich, weil viele unterschiedliche Institutionen auf unterschiedliche Weise die Menge des Geldes vermehren - an erster Stelle die amerikanische Notenbank (FED) und die europäische Zentralbank, dann die Bank von England und die Schweizer Notenbank und viele andere Nationalbanken. Aber auch jede normale Bank kann sich durch Giralgeldschöpfung an der Vergrößerung der Geldmenge beteiligen. Dadurch ist ein Personenkreis involviert, der sich nicht mehr eingrenzen und kontrollieren lässt.

Das wirft einige peinliche Fragen auf:
Wir wissen es nicht. Es ist kein Trost, dass die Tage, Jahre oder Wahlperioden von Frau Merkel gezählt sind. Wenn ihre Nachfolgerin eine Nicht-Physikerin sein sollte, ist auch kein Problem des unendlichen Wachstums gelöst.
Der ungebrochene Glaube an das Wachstum der Märkte und an die Wirtschaftspolitik der Regierungen basiert, wie hier erklärt wurde, auf Unkenntnis funktionaler und mathematischer Zusammenhänge.
Gerade diese Tatsache, dass Naturgesetze von Wissenschaftlern mathematisch formuliert werden und dann unzweifelhaft auch für alle anderen gelten, diese Erkenntnis wird neuerdings gerne ignoriert. Selbst auf höchster Ebene. Es wird versucht, sich durch formalrechtlich gültige Gesetze und Mehrheitsentscheidungen über wissenschaftlich erwiesene Zusammenhänge hinweg zu setzen. Dies geschieht zum Beispiel in der Energiepolitik.
Wind ist eine unzuverlässige Energiequelle und Solarenergie ist vom Sonnenschein abhängig; beides kann durch finanzielle Subventionen und juristisch unanfechtbare Gesetze nicht korrigiert werden. Eine Einschränkung des Energieverbrauchs (und jedes anderen Verbrauchs) dagegen würde zu befriedigenden Ergebnissen führen. Zwischen einer Einschränkung des Energieverbrauchs sowie des Konsums materieller Güter und dem Ausstieg aus dem zwangsläufig exponentiellen Wachstum besteht ein mathematisch eindeutiger Zusammenhang.
Dieser Zusammenhang ließe sich durch andere Funktionen ausdrücken, die eben keine Exponentialfunktionen und damit weniger gefährlich sind als die von Wirtschaft und Politik geforderten Wachstumsfunktionen. Eine mögliche Form von freiwilliger Beschränkung des Energieverbrauchs wird aber nicht diskutiert, weil Selbstbeschränkung beim jetzigen Kenntnisstand nicht mehrheitsfähig ist, weder im Parlament noch in der Bevölkerung.
Weil die Mehrheit der Bevölkerung irrige Ansichten über Energie, Gesundheit, Konsum und Ökologie hat, will man dem pauschal mit "mehr Bildung" begegnen. Das ist falsch, weil unspezifisch. Man muss nicht mehr Geld für Bildung ausgeben, sondern mehr Wissen verbreiten; es kommt auf die Inhalte der Bildung an, auf das Wissen über Fakten und funktionale Zusammenhänge und zwar auch auf Gebieten, die meist unbeliebt sind: Mathematik, Biologie, Physik und Statistik (Statistik ist ein weiteres Beispiel für allgemeine Unkenntnis, die schon an der Schule leicht zu beheben wäre. Das wurde in diesem Essay noch nicht erwähnt, es würde auch zu weit führen.)

Weil Rubikon nicht mehr existiert, ist er hier veröffentlicht.
01.06.2018, Rob Kenius
Letzte Überarbeitung 07.03.2022
Der Eigentümer von Rubikon, Jens Wernicke, hat Rob Kenius als Autor später ausgeschlossen, weil er sich zu wichtig vorkäme, man hätte 400 Autoren. Rob Kenius hatte sich gewünscht, dass man ihm das Erscheinen eines Artikels mitteilt, weil er, falls der Artikel nicht erscheint, ihn auf kritlit.de bringt.(Rubikon verlangte Exclusivität, zahlte aber kein Honorar.)
Nachtrag 2024: Rubikon existiert nicht mehr, weil Jens Wernicke sich Auswanderung nach Südamerika mit Leserspenden hat finanzieren lassen. Die Domain Rubikon ging verloren und die Hiergebliebenen haben das Forum neu gegründet. Rob Kenius schreibt ab und zu für die Neugründung manova.